Автор: Ганашек Александр
Введение
В условиях усложняющихся социально-экономических процессов, требующих использования значительных информационных массивов, использование математического аппарата прогнозирования является перспективным для принятия решений не только правительства, а и основных хозяйствующих субъектов независимо от размеров и сфер деятельности. Является актуальным моделирование национальной экономики для определения возможных направлений развития общества и страны. Кроме того, разработка основных направлений и мероприятий государственной экономической политики в перспективе, а также возможных результатов их осуществления, требует научно обоснованных вариантов развития экономических явлений и процессов.
Макроэкономическая динамика определяется совокупностью сложных процессов. Основные экономические и финансовые показатели, такие как валовый внутренний продукт, уровень производства, уровень безработицы, курсы валют, банковские процентные ставки, курсы ценных бумаг и т. д. повсеместно демонстрируют сложную динамику, сочетающую как временную стабилизацию, так и амплитудные, зачастую апериодические колебания. Функционирование любой экономической системы всегда сопровождается случайными возмущениями как внешними (аддитивными), так и внутренними (параметрическими). Присутствие случайного фактора всегда приводит к деформации режимов динамического поведения исходной детерминированной модели. На значения переменных, участвующих в них, влияет множество факторов, в том числе и политические решения, что существенно усложняет задачу моделирования экономического развития.
Основная часть
В настоящее время разработано и опробовано большое количество математических моделей, позволяющих анализировать экономическое состояние и развитие регионов. Основной недостаток большинства моделей заключается в том, что они являются детерминированными, т. е. в отношении основных величин предполагается их стабильность, случайными воздействиями пренебрегают, таким образом, не учитывается случайный характер воздействия различных факторов. Характер явлений, с которыми приходится иметь дело при исследовании социальных и экономических процессов и управлении ими, требует применения стохастических моделей и методик прогнозирования стохастических систем. Так же необходимо обратить внимание на усложнение социально-экономических процессов в условиях научно-технического прогресса и формирования информационного общества. Как следствие этих явлений, возрос объём количественных и качественных параметров экономических процессов, а потому значительно расширились объем и масштабы прогностической деятельности. В условиях применения технологий, позволяющих обрабатывать значительные массивы информации, возрастает ценность прогнозов и в тоже время увеличиваются возможные негативные последствия реализации определённых решений вследствие ошибочности полученных параметров социально-экономического развития.
В рамках рассматриваемой идеи предлагается:
• учитывать вероятностные процессы и корреляцию влияющих факторов
• исследовать вероятностные свойства аттракторов стохастической системы
• использовать математические и статистические методы для прогнозирования макроэкономических событий
• провести декомпозицию существующих макроэкономических систем, используя эффективные алгоритмы увеличения информативности анализа при обработке данных ограниченного объема
• рассматривать и анализировать критические события в экономической системе как факторы нестабильности стохастической системы
• провести анализ существующих моделей детерминированных и стохастических систем
• рассмотреть перспективность использований нейронной сети с использованием вероятностного метода адаптивного времени вычисления для решения задач моделирования экономических процессов
• изучить вопрос о взаимосвязи микро- и макроэкономических процессов, так как микропроцессы трансформируются в макропроцессы, на основе которых формируется экономическая среда
• изучить равновесие микросостояния в системах со стохастическим поведением элементов
• определение оптимальных исходных данных о параметрах моделируемой системы
На данном этапе были проведены исследования методов прогнозирования стохастических систем, а также их математических моделей. Разработан и прошел апробацию общий математический аппарат по учету и прогнозирования влияющих факторов в стохастической системе. Ставятся следующие цели:
• разработка концепции и архитектуры системы математического моделирования национальной экономики путем прогнозирования макроэкономических событий
• создание базового комплекса математических моделей, алгоритмов для поддержки анализа стохастической системы.
• разработка и использование программного обеспечения для поставленных ранее целей.
Также обращаю внимание на финансовый анализ с помощью искусственных нейронных сетей (ИНС), рассматриваемых как механизм реконструкции репрезентативного агента, принимающего решения, и благодаря своим отличительным характеристикам ИНС могут быть использованы для прогнозирования доходности на фондовом, валютном и других рынках. Отдельная важная проблема в рамках исследований искусственных нейронных сетей и повышения эффективности их прогнозных способностей – это различные способы обработки входных данных. Это объясняется тем, что в последние годы массивы данных, доступные финансовым аналитикам, существенно возросли, а взаимосвязи между ними, в том числе причинно-следственные, усложнились.
Проведенный анализ показал, что существующие методы прогнозирования не обладают требуемой точностью, а существующий математический аппарат не позволяет обеспечить достижение поставленных задач. Необходим поиск эффективных методик прогнозирования, проведем их общий анализ.
Методология аналитического прогнозирования направлена на получение математической модели системы, соответственно, обеспечивается высокая точность прогнозирования, но только при наличии достаточного количества априорной информации об исследуемых объектах и протекающих в них процессах. Аналитическое прогнозирование не учитывает случайный характер внешних и внутренних воздействующих факторов, также необходимо учитывать значительную неопределенность процессов и случайный характер воздействий со стороны внешней среды. В результате представляется актуальным рассмотрение методов вероятностного прогнозирования [1].
Рисунок 1 – Аналитическое прогнозирование
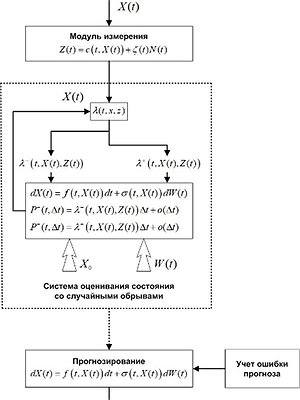
Вероятностные методы прогнозирования позволяют учитывать случайный характер процессов стохастической системы под влиянием внешних и внутренних факторов, а также погрешности при расчете прогноза. Однако нестационарность сложных систем ограничивает применение статистических моделей, которые требовательны к объему анализируемых данных и не подходят для работы с динамическими процессами.
Рисунок 2 – Вероятностное прогнозирование
Методы статистической классификации опираются на аппарат теории распознавания образов и построения искусственных нейронных сетей. Для обучения нейронной сети требуется значительный объем времени и априорной информации. Результаты анализа показали, что абсолютно эффективной методологии прогнозирования не существует.
Все физические объекты и процессы являются стохастическими, т. е. их характеристики носят случайный характер. При описании объектов как детерминированных систем в качестве характеристик элементов используется их математическое ожидание [14-16]. Однако при более строгом подходе их нужно принимать как стохастические, считая характеристики элементов случайными функциями, в стохастических системах изменения носят случайный характер, в которых предсказываемые значения зависят от распределения вероятностей.
Рисунок 3 – Прогнозирование на основе статистической классификации
В случаях, когда значительная стохастическая составляющая препятствует применению детерминированных подходов, нередко прибегают к выделению и статистическому анализу псевдостацинарных участков процессов, протекающих в анализируемой системе. Однако, в зависимости от степени нестационарности, такие участки не всегда имеют достаточную длительность для набора представительной статистики [3-8]. Из этого факта неизбежно вытекает необходимость поиска эффективных алгоритмов и методов увеличения информативности анализа при обработке выборок. Особенностью последнего периода развития статистических методов исследования является широкое применение вычислительной техники при обработке данных. Современные методы обработки информации свободны от многих допущений благодаря возможности интенсивного численного анализа, рандомизации, программного комплекса и компьютерного моделирования.
В последние годы в мире наблюдается рост объёмов собираемых данных. В связи с этим возрастает актуальность методов машинного обучения, позволяющих автоматически извлекать закономерности из данных.
В задачах машинного обучения предполагается, что объекты реального мира описаны с помощью признаков, а также что имеется обучающая выборка, полученная из генеральной совокупности объектов.
Популярным способом решения задач машинного обучения является вероятностное моделирование. В случае обучения с учителем вероятностная модель задаёт распределение над метками при условии наблюдаемых данных. Для обучения без учителя в модель, как правило, вводятся латентные (ненаблюдаемые) переменные, определяющие факторы вариации данных. Параметры вероятностной модели настраиваются при помощи метода максимального правдоподобия, используя обучающую выборку и градиентные методы оптимизации. Во многих случаях правдоподобие модели с латентными переменными не может быть подсчитано аналитически. Тогда применяются вариационные методы, такие как вариационная нижняя оценка на правдоподобие. Успех методов машинного обучения принципиально зависит от информативности признакового описания объектов. Одними из наиболее сложных с точки зрения построения признакового описания объектами являются высокоразмерные неструктурированные данные.
В последние годы глубинное обучение (deeplearning) стало наиболее эффективным способом работы с высокоразмерными неструктурированными данными. Глубинное обучение предлагает использовать многослойные(глубинные)признаковые описания объектов, задаваемые нейросетями с десятками и сотнями слоёв. При этом архитектура нейросети выбирается исходя из особенностей данных. Однако вычисления с помощью глубинного обучения стали затратны из-за возросшего числа слоев. Одним из способов сокращения объёма вычислений является вероятностное адаптивное определение объёма вычислений для каждого объекта [9]. В его основе лежит вероятностная модель, в которой дискретные латентные переменные задают число выполняемых итераций. Априорное распределение на латентные переменные определяет желаемое соотношение между скоростью и качеством вычислений. Вероятностный метод адаптивного времени вычислений (ВАВВ) в отличии от АВВ может быть использован в стохастических системах, так как итоговый функционал является не разрывной функцией. Чтобы приблизиться к целевой функции и не допустить разрыва используем стохастическую вариационную оптимизацию.
Рассмотрим целевую функцию вариационной оптимизации , где z – случайная величина, - предложенное распределение с параметрами . Стохастическая вариационная оптимизация позволяет оценить градиент стохастически, даже если математическое ожидание не вычислимо аналитически, либо имеет слишком высокую стоимость вычисления. Сначала рассмотрим случай репараметризуемых распределений, а затем перейдём к случаю дискретных распределений [2].
Пусть распределение является репараметризуемым. В таком случае стохастические градиенты могут быть получены при помощи трюка репараметризации. К этим градиентам могут быть применены методы стохастической градиентной оптимизации, что позволяет произвести стохастическую оптимизацию целевой функции.
Предположим теперь, что z - дискретная случайная величина, тогда:
, (1)
где c – скалярная величина, называемая базовой функцией награды. Мат. ожидание может быть приближено с помощью метода Монте-Карло. Эта процедура позволяет получить несмещённые градиенты, однако оценка обычно имеет слишком высокую дисперсию .
Применим релаксацию Гумбель-Софтмакс к предложному распределению, а затем воспользоваться трюком репараметризации . Это приводит к градиентам с низкой дисперсией ценой некоторого систематического смещения [20-22].
Предположим, что ,пользуясь правилом произведения для вероятностных распределений, преобразуем предложенное распределение:
(2)
Этот приём позволяет генерировать точки z. Сделаем два предположения:
1. Функция непрерывно дифференцируема при ;
2. Каждый фактор , непрерывно дифференцируем при . При условии этих предположений можно применить релаксацию Гумбель-Софтмакс с температурой > 0 к каждому фактору:
(3)
Релаксированная целевая функция имеет вид:
(4)
Полученная целевая функция может быть стохастически оценена с помощью метода Монте Карло. Заметим, что если все вероятности в релаксированном распределении приближаются к крайним значениям (нулю или единице), то релаксированное распределение приближается к нерелаксированному при любой температуре . Отсюда следует, что величина релаксированной целевой функции ) приближается к значению исходной целевой функции , что делает вероятностный метод адаптивного времени вычислений одним из наиболее эффективных и точных подходов для сокращения объемов вычисления в стохастических системах [17-19].
Одной из самых распространенных моделей стохастических систем является модель на базе цепей Маркова. Марковские цепи представляют собой непараметрическую модель (многомерную гистограмму) в форме многомерного распределения, которое, в общем случае, может изменяться во времени. Управляемые цепи Маркова учитывают влияние управляющих входных сигналов на поведение стохастической системы.
Для построения стохастической модели используем данные о любом процессе в экономике, которые заносим в Марковскую матрицу. Размер матрицы определяется априорной информацией о порядке модели объекта и числом интервалов и [10-13]. Вероятности переходов оцениваются как относительные частоты соответствующих событий. Статистическая оценка переходных вероятностей управляемой марковской цепи сводится к подсчету соответствующих событий за время наблюдения и последующему вычислению элементов матрицы по формуле:
(5)
где – число событий вида , а знаменатель соответствует числу событий вида . Таким образом, при любой комбинации состояния и управления получаем полную систему событий, заключающихся в переходах в состояния . Нормализация делает матрицу стохастической.
В результате набор вероятностей по каждой строке описывает полную систему событий, для которых сумма вероятностей равна единице:
Распределение вероятностей нового состояния системы при заданных и определяется соответствующей строкой матрицы .
Моделирование координат состояния по марковским моделям производится с использованием метода Монте-Карло и метода функционального преобразования. Для этого на каждом шаге моделирования определяется текущее состояние и текущее управление . Затем находят распределение и вычисляют интегральную функцию распределения :
(6)
(7)
Получаем двумерный массив данных представленный в виде таблицы в которой n-строк и m-столбцов, а под ячейкой таблицы, стоящей в -й строке и -м столбце понимают некоторый элемент массива с координатами .
Рисунок 4 – Вероятностное поле на базе матрицы Маркова
Данный массив используется для вычисления прогнозируемых частот отказов в разработанном программном обеспечении.
Функциональным назначением прикладного программного обеспечения является автоматизация статистических методов решения задач первичной обработки данных и вычисления элементарных статистик в процессе управления рисками, а также загрузку и ведение базы данных, ориентированной в последующем на принципы машинного обучения. Представленный функционал реализует оценку частот возникновения определенных событий в прошлом на основе статистических данных (данные, накопленные за некоторый период эксплуатации элементов системы) и прогнозирование частот, с которыми эти события станут возникать в будущем. Обрабатываемые на входе данные представлены в виде двумерного массива переменной размерности. Информация считывается в рабочую таблицу данных формата dbf и в последующем является источником данных для создания необходимых для реализации алгоритма новых таблиц данных. Основные и наиболее трудоемкие операции реализованы через команду select. Агрегирование, консолидация и вычислительные операции значений переменных производится вышеуказанной программной единицей с опцией group by. Основная задача программы построение описательных критериев текущей выборки с целью выработки прогнозного массива значений исследуемых переменных. Ниже приведем перечень выстраиваемых основных вероятностных критериев:
• количество выпадений (появлений) переменной в выборке;
• интервалы выпадения;
• прогноз числа (чисел), следующего за каждым рассматриваемым последним числом в выборке и прогноз предшествующего числа (чисел) рассматриваемому числу;
• учет как отношения сумм нечетного/четного числового признака в строках исходного массива;
• суммирование чисел в строках для анализа динамики роста или убывания признака, а также определения наиболее частого интервала сумм;
• формирование аналитического отчета по наиболее частым сочетаниям цифр (реализовано по трем числам);
• расчет погрешности прогноза.
Представления перечисленных критериев представлены как в отчетном, так и графическом формате. Графическая адаптация представлена в виде конечных жестких графиков, а также доступна в рамках конструктора с привязкой полей визуальной рабочей таблицы к координатным осям X и Y. Спецификация актуального графического ландшафта определена типом графика bar line и фильтром по выбранной колонке входного массива.
Более подробно остановимся на расчетном блоке погрешности прогноза. Допустим мы хотим проанализировать выборку объемом рядом из 100 чисел. По умолчанию начальная позиция в выборке для запуска исчисления погрешности задается на уровне 75% объема начальной выборки. Начиная с 75-ой позиции по каждой последующей рассчитывается прогнозный массив чисел параллельно по двум направлениям. В первом случае прогнозное число становится последующим элементом выборки. Во втором случае прогноз остается прогнозом, расчет продолжается на основе рассчитываемых чисел. Ввиду того, что как правило мы имеем массив прогнозов для получения уникального прогнозного числа применяем принцип идентификации по максимальной частотности признака. В конечном счете результатом работы данного блока является рассчитанная средняя погрешность прогноза.
В результате опытной эксплуатации программы была получена точность прогноза до 80 %.
Формула прогнозирования частот:
(8)
Рисунок 5 – Интерфейс прикладного программного обеспечения
Основные вычислительные транзакции:
• прогнозная
select vari,vari+1,max(n) maxi from (select vari,vari+1,count(*) n from (select vari,vari+1 from (select vari,i, count(*) n from cursor a group by vari,i) b left join cursor a ON bi+1=ai) group by vari,vari+1) group by vari,vari+1.
• вычисление значений промежуточных индикаторов
select * from (select ft,ro,count(*) s from st001 group by ft,ro where ro>= w and ro<= w+ st- 1) b left join st001 a on b.ro-1=a.ro into table st005
select * from (select ft,ro,count(*) s from st001 group by ft,ro where ro>= w and ro<= w+ st- 1) b left join st001 a on b.ro+1=a.ro into table st005.
Точность прогноза = Maximum of (1 – Ошибка, 0),
где Ошибка:
. (9)
в качестве основной ошибки для расчета точности прогнозирования мы будем использовать Взвешенную Абсолютную Процентную Ошибку (WAPE – Weighted Absolute Percent Error), которая рассчитывается по формуле (15).
Приведем структуру отчетов по блоку машинного обучения, они содержат группы по числу столбцов входного файла.
Рисунок 6 – Аналитический отчет блока машинного обучения
Структура одной группировка, следующая:
1) Индекс элемента выборки.
Генеральная выборка как правило 100 позиций, регрессивный анализ машинного обучения начинаем с 85-ого индекса;
2) Средняя(факт-прогноз)
По каждому элементу прогнозного массива с индексом от 85 до 100 берется разница с фактом и далее рассчитывается средняя величина данных отклонений;
3) Прогноз=факту
Элемент прогнозного массива совпал с фактом
4) 1<= (факт-прогноз) =<1(%)
В рамках каждой прогнозной выборки находим количество отклонений прогноза от факта по заданному условию: в нашем случае данное отклонение не должно превышать единицы. В отчете показывается удельный вес в % найденных величин.
Простейшая модель машинного обучения строится на решении задач определения зависимости частотных характеристик переменных генеральной выборки, с целью прогнозирования дальнейшего поведения данных переменных (регрессии). Далее приведем две основные конструкции:
IIF(ar7< ar3,UPDATE tp_fn set tp=tp_fn,vr1=ar3 WHERE ALLTRIM(r0.cn)$cn)
SELECT ft_a,ft_b,&tp_fn(ct) FROM s7 INTO CURSOR s9 GROUP BY ft_a,ft_b
В первой программной конструкции формируется информация о наиболее выигрышной итоговой стратегии, а во второй мы видим ее же применение при сборке окончательного прогнозного массива.
Алгоритм работы программы:
1) Проводим парный регрессивный анализ каждой из итерационных выборок / с 85 по 100 / по MAX и MIN стратегии. То есть, прогнозные массивы формируются на основе вычисления максимальных или минимальных частот последующих и предыдущих элементов текущей выборки.
2) Анализируем прогнозную эффективность MAX и MIN стратегий по параметру прогноз=факту и считаем результатом данного машинного обучения следующее: из прогнозных положительных результатов в случае их фиксации в данной колонке выбираем наиболее результативную модель MAX или MIN ( Колонки B,C,D, F). В противном случае, в колонке Е имеем нулевой результат и в дальнейшем будем считать, что для формирования выходного прогнозного массива целесообразно принять принцип множественной регрессии. То есть, частотный анализ будет охватывать все элементы текущей выборки, а прогнозный массив строится на основе вычисления максимальных частот отклонений частоты каждого элемента выборки от частоты элемента с минимальной величиной.
Методология показывает достаточно высокую точность прогноза (60–100%), примененный программно-технологический аппарат позволяет развивать, применять и автоматизировать на практике статистический функционал проекта.
Заключение
Существующие системы анализа и прогнозирования процессов в экономике не учитывают вероятностный характер процессов, протекающих в системе. Рассматривая макроэкономические явления в стохастической системе, открывается возможность учитывать корреляцию между экономическими факторами, а также случайную составляющую событий (пандемии, техногенные катастрофы), которые могут серьезно усложнять точность и объективность анализа и прогнозирования состояния национальной экономики. Также в стохастической системе все предсказанные значения зависят от распределения вероятностей, предложенные методы точно описывают область значений случайной величины и соответствующие вероятности появления этих значений, даже в ситуации, когда объем обрабатываемых данных ограничен или слишком велик.
Список использованных источников
1. Горбунова Е. Б. Метод статистической обработки малых выборок данных в задачах прогнозирования и контроля состояния сложных систем: диссертация, Таганрог: ЮФУ, 2017. —151 с.
2. Фигурнов М. В. Вероятностный метод для адапативного времени вычислений в нейронных сетях: диссертация, Москва: Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский университет «Высшая школа экономики», 2019. — 116 с.
3. Авдийский В. И., Курмашов Ш. Р. Прогнозирование и анализ рисков в деятельности хозяйствующих субъектов: монография / под общ. ред. М. А. Эскиндарова. — М.: ФА, 2003. – 392 с.
4. Брандт З. Статистические методы анализа наблюдений. – М.: Мир, 1975. – 312 с.
5. Вентцель Е.С. Овчаров Л.А. Теория случайных процессов и её инженерные положения: учеб. пособие для втузов 2-е издание М.: Высшая школа, 2000. – 383 с.
6. Вентцель Е.С. Теория вероятностей: Учеб. для вузов. – 6-е изд. стер. – М.: Высш. шк., 1999. – 576 c.
7. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и её инженерные положения – учеб. Пособие для втузов 2-е издание М.: Высшая школа, 2000. – 383 с.
8. Волков И.К., Зуев СМ., Цветкова Г.М. Случайные процессы: учеб. для вузов / под ред. B.C. Зарубина, А.П. Крищенко. М.: Изд-во МГТУ им. Н.Э. Баумана, 1999. 448 с. (Сер. Математика в техническом университете; Вып. XVIII).
9. Галушкин А. Нейронные сети: основы теории. Горячая Линия-Телеком, 2010. – 480 с.
10. Гмурман В.Е. Теория вероятностей и математическая статистика 9-е изд., стер. – М.: Высшая школа, 2003. – 479 с.
11. Золоторев В.М. Современная теория суммирования независимых случайных величин. – М.: Наука., 1986. – 416 с.
12. Иглин С.П. Теория вероятностей и математическая статистика на базе MATLAB.: учебное пособие. – Харьков: НТУ «ХПИ», 2006. – 216 с.
13. Маталыцкий М.А. Элементы теории случайных процессов: учеб. пособие. Гродно: ГрГУ, 2004. 326 с.
14. Назаров А.А., Терпугов А.Ф. Теория вероятностей и случайных процессов: учеб. пособие. 2-е изд., испр. Томск: Изд-во НТЛ, 2010. 204 с. 5.
15. Неделько С.В., Неделько В.М., Миренкова Г.Н. Типовые задачи математической статистики – Изд-во НГТУ, 2014. – 52 с.
16. Феллер, В. Введение в теория вероятности и её приложения Т. 1: Пер. с англ. – М.: Мир, 1984. – 528 с.
17. Gal Y., Ghahramani Z. A theoretically grounded application of dropout in recurrent neural networks // Advances in neural information processing systems. — 2016.
18. Gal Y., Ghahramani Z. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning // International Conference on Machine Learning. — 2016. — P. 1050–1059.
19. Kachala, V.V. Fundamentals of systems theory and systems analysis. – M: Goryachaya liniya-Telekom, 2007. – 216 p.
20. Srivastava N., Hinton G., Krizhevsky A., Sutskever I., Salakhutdinov R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting // Journal of Machine Learning Research. — 2014.
21. Veit A., Belongie S. Convolutional Networks with Adaptive Computation Graphs // arXiv. — 2017
22. Wu Z., Nagarajan T., Kumar A., Rennie S., Davis L. S., Grauman K., Feris R. BlockDrop: Dynamic Inference Paths in Residual Networks // arXiv. — 2017
Приложения